Etage is a data-flow based programming language. It is build upon Haskell and provides nondeterminism and laziness. It is text based and through few basic commands it allows defining operations (neurons) and connections between operations (nerves) along which data can flow. Moreover, program can form a network with loops and is not limited to only tree-like structure.

Introduction

Current mainstream programming languages are based on the control-flow concept. They are series of instructions to compute, modify memory, do IO, which more or less abstract another similar series of instructions running on a CPU. While there are many variations and ways of abstraction of control-flow programs, there is another way how to specify a program and this is by defining how data flows in the program, instead of defining how control flows. Such programs are data-flow programs.

In the past there were attempts at data-flow computer architecture, like Manchester Dataflow Machine, but have not managed to outperform control-flow processors and architecture and gain wide acceptance. Nevertheless, we can still design a data-flow programming language which is then compiled and executed on a control-flow architecture.

Motivations for expressing a program in a data-flow manner are multiple. Sometimes a problem itself is easier described in a data-flow manner. Sometimes we can discover and gain performance advantages by explicitly defining and isolating interactions between data in the program, which helps automatically parallelizing programs to multi-core architecture. Our motivation was to be able to easier model complex behaviors of high-level neural and signal networks found in nature. If you observe how signals travel from senses to brain and back to muscles in an animal, you notice that behavior is closer to data-flow than control-flow.

We implemented our data-flow programming language Etage as a framework on top of Haskell programming language. Haskell is a lazy functional programming language with many bleeding-edge concepts and serves well as a host. Main features we find useful are support for lightweight threads called sparks which can be automatically parallelized and a powerful type system which allows checking if our data-flow program has correctly connected flows. The downside is that syntax itself is directed and limited by that of Haskell, so programs are sometimes more verbose than they would have to be with specific syntax. We could address some of these issues with a preprocessor stage. Etage is open source and is available as a Haskell package and it comes with extensive documentation. In this paper we present its design.

Example

To easier understand how our programming language works, see the following example program, a program which outputs series of Fibonacci numbers, as a control-flow and data-flow programs.

a := 0
b := 1
repeat:
    print b
    c := b
    b := b + a
    a := c

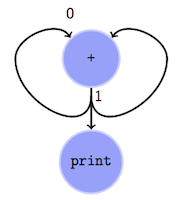
Data-flow program is shown graphically for easier understanding. It consist of neurons (also known as operators) and directional nerves (connections between operators). Neurons can be arbitrary computations which receive zero or more inputs and have zero or more outputs.

Observe that in our case data-flow programs can contain loops. See that the data-flow program first prints \(1\) because print neuron is the only one which has data on all its inputs, and at the same time that \(1\) is send back to inputs of + neuron, once to each input. Now + neuron has both \(0\) and \(1\) as inputs (including one more \(1\) waiting after \(0\)) and outputs new \(1\). Data flows again and next time it outputs \(2\) and so on, the print neuron printing those outputs as they come. With correct arrival order of data to + neuron inputs we achieved summation of previous and current value.

incubate $ do
  nerveDump <- (growNeuron :: NerveOnlyFor DumpNeuron) defaultOptions
  nerveSum <- (growNeuron :: NerveBoth (FunctionNeuron IIntegerList IInteger))
                (\o -> o { function = fibSum })

  liftIO $ do
    t <- getCurrentImpulseTime
    sendFromNeuron nerveSum $ IValue t 0

  nerveSum' <- liftIO $ branchNerveFrom nerveSum
  nerveFused <- [TranslatableFrom nerveSum, TranslatableFrom nerveSum']
                  `fuseWith` listFuser

  nerveSum `attachTo` [TranslatableFor nerveDump]
  nerveFused `attachTo` [TranslatableFor nerveSum]

  liftIO $ do
    t <- getCurrentImpulseTime
    sendFromNeuron nerveSum $ IValue t 1

The same program in our programming language Etage. While before we shown a graphical representation of the program, programming language Etage is text based and you describe neurons and nerves as a series of command to create them and connect them together.

First we invoke our monad which encapsulates all logic of growing neurons and connecting them together, and waiting for them to finish. Then we create (grow) two neurons. We determine which neurons we create by specify the return type of the growNeuron function. Additionally, we have to specify if nerve attached to the neuron should serve only as input, only as output, or both, some neurons can work in different configurations. By explicitly stating this, type system can help us verify if we are using neurons as expected. DumpNeuron has only one input and it prints any input to the console. FunctionNeuron has both input and output. It is defined as a general neuron which takes a function to run on inputs to get next output. In our case our function fibSum receives a list of integers (two in our case) as input and returns one integer, sum of input integers. (Definition is omitted for brevity.)

Then we prepopulate input of FunctionNeuron with \(0\), after which we branch nerveSum and fuse it together back. This makes nerveFused in fact be two nerves, in a similar way that our graphical representation shows how each output goes back to FunctionNeuron twice. We then connect output to DumpNeuron, and duplicated one back as inputs to FunctionNeuron. We start everything by pushing \(1\) as next input.

This example looks a bit complicated and this is truthfully so because it tries to showcase multiple features of our programming language at the same time. In reality, we would not program like this and we would simply use DelayNeuron to delay input for one value, allowing easy summation of previous and current value.

Type system checks if types of inputs match types of outputs, or at least that there is translation defined between output and input types. For this we are using an existentially quantified types TranslatableFrom and TranslatableFor encompassing all nerves which can be translated to and from the same data type, respectively. Translators between data types can be defined through Haskell’s type class system which allows great modularity.

Related work

There are many production systems build upon data-flow programming model, but most of them are visual: PureData, Max, LabVIEV, or abstract systems: MillWheel¹. But all those data-flow implementations are deterministic. We decided to design out programming language without any guarantees on determinism to allow easier parallelization of its execution. If needed, determinism can be build upon our programming language with concepts like token-passing.

In addition, our data-flow programming language is lazy with an interesting property that information about data traverses nerves in an eager manner which invokes neurons to run immediately when data is available on their inputs, but data value is computed only if needed in a lazy manner which means that computation itself in a way back-propagates to previous neurons to compute their computation necessary for computing resulting value.

While other data-flow systems forces operations to be assembled in a tree-like structure, out programs can be arbitrary networks with loops if necessary. Programming language does not provide any guarantees about program termination and bounds on memory consumed by data accumulating in nerves if neurons are consuming data slower than other neurons are producing data. In theory nerves are unbounded, in practice they are limited by memory available. Correct programs should probably never have a nerve growing in size constantly.

Design

class (Typeable n, Impulse (NeuronFromImpulse n),
       Impulse (NeuronForImpulse n), Typeable (NeuronFromImpulse n),
       Typeable (NeuronForImpulse n)) => Neuron n where
  type NeuronFromImpulse n
  type NeuronForImpulse n
  data NeuronOptions n

  mkDefaultOptions :: IO (NeuronOptions n)

  getNeuronMapCapability :: NeuronOptions n -> NeuronMapCapability

  grow :: NeuronOptions n -> IO n
  live :: Nerve (NeuronFromImpulse n) fromConductivity (NeuronForImpulse n)
    forConductivity -> n -> IO ()
  dissolve :: n -> IO ()

  attach :: (NeuronOptions n -> NeuronOptions n) ->
    Nerve (NeuronFromImpulse n) fromConductivity (NeuronForImpulse n)

Design of a programming language is based on two basic concepts: neurons and nerves.

You define neurons with input and output types and computation which is run when input data is available. Neurons can keep arbitrary internal state. Neurons can also do IO operations. IO operations can in this way be easily encapsulated without other neurons having to know about the nature of IO operation. Computation done by a neuron can be programmed in Haskell or another data-flow program. Neurons are defined as Haskell class types where one has to define mainly grow, dissolve and live methods for three stages in a life cycle of a neuron.

growNeuron :: (Neuron n,
  GrowAxon (Axon (NeuronFromImpulse n) fromConductivity),
  GrowAxon (Axon (NeuronForImpulse n) forConductivity)) =>
  (NeuronOptions n -> NeuronOptions n) ->
    Incubation (Nerve (NeuronFromImpulse n) fromConductivity
                      (NeuronForImpulse n) forConductivity)

attachTo :: forall from for forConductivity. (Impulse from, Impulse for) =>
  Nerve from AxonConductive for forConductivity -> [TranslatableFor from] ->
  Incubation ()

fuseWith :: forall i j. (Impulse i, Impulse j) =>
  [TranslatableFrom i] -> (ImpulseTime -> [i] -> [j]) ->
  Incubation (Nerve (FuseFromImpulse i j) AxonConductive

Nerves are predefined and serve to connect neurons together. You can attach them to nerves, branch them and fuse them together to create arbitrary networks of nerves between neurons. Nerves operate in FIFO manner and have guaranteed order.

Data types send around the program can be extended through type class. Various neurons can support various data types and to assure compatibility between various neurons, explicit translator class type instance can be defined. In this way Haskell knows how to automatically translate between various data types as needed.

Conclusion

While presented programming language promises an alternative approach to programing data-flow programs through text based programming and offers features like nondeterminism and laziness, it has to our knowledge not yet been used in a larger program to really determine usefulness of these features. Moreover, it has not yet been used to model high-level neural and signal networks, what was our initial motivation. On the other side, design seems possible to implement and implementation was successfully stress tested. Extensive use of Haskell type system allows compile time verification of data-flow programs and assurance that inputs and outputs are correctly connected.